What is the time complexity of the following function in terms of \(n\)? State your answer using asymptotic notation (e.g., \(\Theta(n)\)).

def foo(n):
    i = 0
    while i < n**2:
        i = i + 2
        j = 0
        while j < n:
            for k in range(n):
                print(i + j + k)
            j = j + 10

What is the time complexity of the following function in terms of \(n\)?

def foo(n):
    for i in range(n**2):

        for j in range(i):
            print(i+j)

        for k in range(n):
            print(i+k)

        for x in range(n - i):
            print(x)

What is the time complexity of the following function in terms of \(n\)?

from math import sqrt, log, ceil

def foo(n):
    for i in range(ceil(n**3 - 10*n + sqrt(n))):
        for j in range(ceil(log(n**2))):
            print(i, j)

What is the time complexity of the following function in terms of \(n\)?

def foo(arr):
    """`arr` is a list containing n numbers."""
    for x in arr:
        if x > max(arr) / 2:
            print('large!')
        elif x < min(arr) * 2:
            print('small!')
        else:
            print('neither!')

What is the time complexity of the following function?

import math

def foo(n):
    for i in range(math.floor(math.sqrt(n))):
        for j in range(math.floor(5*n**2 - math.sqrt(n)/1_000_000 + 100)):
            print(n * n)

What is the time complexity of the following function?

def foo(arr):
    """`arr` is an array with n elements."""
    x = max(arr) * min(arr)
    if sum(arr) > 10:
        return x
    else:
        return 0

What is the time complexity of the following function?

def foo(n):
    i = 0
    while i < n:
        j = 0
        while j < i:
            print(i + j)
            j += 1
        i += 5

What is the time complexity of the following function? State your answer using asymptotic notation (e.g., \(\Theta(n)\)).

def foo(n):
    for i in range(n):
        for j in range(n):
            for k in range(n**2):
                print(i + j + k)

What is the time complexity of the following function? State your answer using asymptotic notation (e.g., \(\Theta(n)\)).

def foo(n):
    for i in range(n):
        for j in range(n**2):
            for k in range(n):
                print(i + j + k)

Express the time complexity of the following code using asymptotic notation in as simplest terms possible.

def foo(n):
    for i in range(200, n):
        for j in range(i, 2*i + n**2):
            print(i + j)

Express the time complexity of the following code using asymptotic notation in as simplest terms possible.

import math

def foo(arr):
    """`arr` is an array with n elements."""
    n = len(arr)
    ix = 1
    s = 0

    while ix < n:
        s = s + arr[ix]
        ix = ix * 5 + 2

    return s

Express the time complexity of the following code using asymptotic notation in as simplest terms possible.

def foo(n):
    for i in range(n):
        for j in range(i):
            for k in range(n):
                print(i + j + k)

Express the time complexity of the following code using asymptotic notation in as simplest terms possible.

def foo(n):
    for i in range(n**3):
        for j in range(n):
            print(i + j)
        for j in range(n**2):
            print(i + j)

Suppose bar and baz are two functions. Suppose bar's time complexity is \(\Theta(n^3)\), while baz's time complexity is \(\Theta(n^2)\).

Suppose foo is defined as below:

def foo(n):
    if n < 1_000:
        bar(n)
    else:
        baz(n)

What is the asymptotic time complexity of foo?

The function below counts how many elements What is the time complexity of the following function in terms of \(n\)? Remember to state your answer in the simplest terms possible.

from math import sqrt, log, ceil

def foo(n):
    for i in range(ceil(n**3 - 10*n + sqrt(n))):
        for j in range(ceil(log(n**2))):
            print(i, j)

What is the time complexity of the following function in terms of \(n\)?

def foo(arr):
    """`arr` is a list containing n numbers."""
    for x in arr:
        n = len(arr)
        if x > sum(arr) / n:
            print('large!')
        elif x < sum(arr) / n:
            print('small!')
        else:
            print('neither!')

What is the time complexity of the following function in terms of \(n\)?

import math

def foo(n):
    for i in range(math.floor(math.sqrt(n))):
        for j in range(i):
            print(i + j)

What is the time complexity of the following function in terms of \(n\)? State your answer using asymptotic notation (e.g., \(\Theta(n)\)).

def foo(n):
    for i in range(n**3):
        for j in range(n):
            print(i + j)
    for k in range(n):
        for l in range(n**2):
            print(k * l)

Suppose bar and baz are two functions. Suppose bar's asymptotic time complexity is \(\Theta(n^4)\), while baz's is \(\Theta(n)\).

Suppose foo is defined as below:

def foo(n):
    if n < 1_000_000:
        bar(n)
    else:
        baz(n)

What is the asymptotic time complexity of foo?

Solution

\(\Theta(n)\) If you were to plot the function \(T(n)\) that gives the time taken by foo as a function of \(n\), you'd see something like the below:

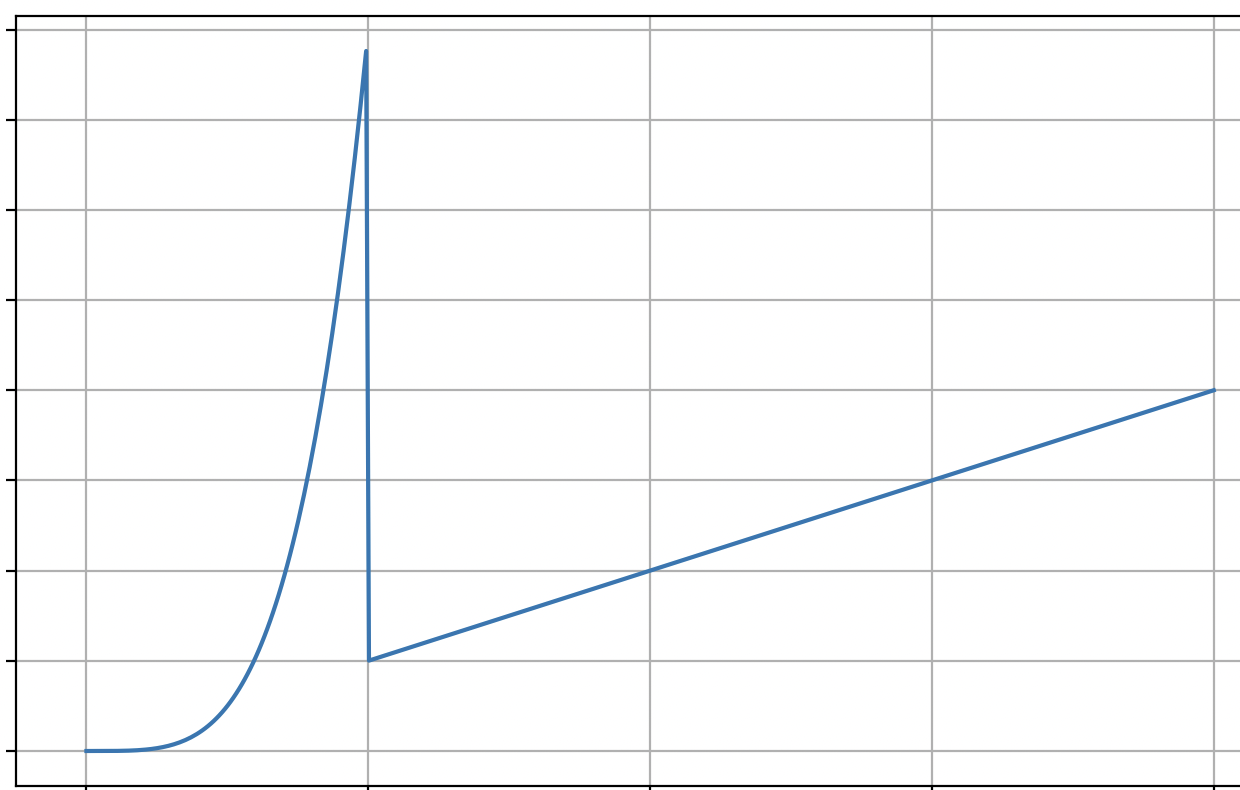
This function starts off looking like \(n^4\), but at \(n = 1_000_000\), it "switches" to looking like \(n\).

Since asymptotic time complexity is concerned with the behavior of the function as \(n\) gets large, we can ignore the part where \(n\) is "small" (in this case, less than \(1{,}000{,}000\)). So, asymptotically, this function is \(\Theta(n)\).

Suppose bar and baz are two functions. Suppose bar's time complexity is \(\Theta(n^2)\), while baz's time complexity is \(\Theta(n)\).

Suppose foo is defined as below:

def foo(n):
    # will be True if n is even, False otherwise
    is_even = (n % 2) == 0
    if is_even:
        bar(n)
    else:
        baz(n)

Let \(T(n)\) be the time taken by foo on an input of sized \(n\). True or False: \(T(n) = \Theta(n^2)\).

What is the time complexity of the following function? State your answer as a function of \(n\) using asymptotic notation in the simplest form possible. (e.g., \(\Theta(n)\))

def boo(n):
    for i in range(200, n):
        for j in range(i, i * n):
            print(i + j)

boo(202)

\(\Theta(n^3)\) Show Answer

What is the time complexity of the following function? State your answer as a function of \(n\) using asymptotic notation in the simplest form possible. (e.g., \(\Theta(n)\))

import math

def boo(n):
    i = n
    while i > 1:
        i = i / 2
        for j in range(1_000_000):
            print(i + j)

boo(100)

\(\Theta(\log n)\) Show Answer

What is the time complexity of the following function? State your answer as a function of \(n\) using asymptotic notation in the simplest form possible. (e.g., \(\Theta(n)\))

import math

def boo(n):
    for i in range(n):
        for j in range(n):
            print(i + j)

    for i in range(math.floor(math.sqrt(n))):
        for j in range(math.log2(i), i * math.floor(math.log2(i + 10))):
            print(i + j)

\(\Theta(n^2)\) Show Answer

import math

def mediansort(arr, start, stop):
    """Claims to sort the array, in-place"""
    if stop - start <= 1:
        return

    # finds the index of the median of arr[start:stop]
    median_ix = find_median(arr, start, stop)

    middle_ix = math.floor((start + stop) / 2)

    # move the median to the middle by swapping
    arr[median_ix], arr[middle_ix] = arr[middle_ix], arr[median_ix]

    # recurse on the left and right halves
    mediansort(arr, start, middle_ix)
    mediansort(arr, middle_ix + 1, stop)

Consider the mediansort function from above. Suppose that find_median takes \(\Theta(n)\) time. What is the time complexity of mediansort?

\(\Theta(n \log n)\) Show Answer

What is the expected time complexity of the following function? State your answer using asymptotic notation.

import random

def boo(n):
    # draw a number uniformly at random from 0, 1, 2, ..., n-1 in Theta(1)
    x = random.randrange(n)

    for i in range(x): # <-- note that the range is random!
        print(i)

\(\Theta(n)\) Show Answer

What is the time complexity of the following function? State your answer as a function of \(n\) using asymptotic notation in the simplest form possible. (e.g., \(\Theta(n)\))

import math
def boo(n):
    for i in range(n):
        for j in range(n**2 + 100, 500*n**3):
            for k in range(1_000, math.floor(math.log(n))):
                print(i + j + k)

boo(100)

\(\Theta(n^4 \log n)\) Show Answer

Suppose bar and baz are two functions. Suppose bar's time complexity is \(\Theta(n^3)\), while baz's time complexity is \(\Theta(n^2)\).

Suppose boo is defined as below:

def boo(n):
    if n < 1000:
        bar(n)
    else:
        baz(n)

What is the asymptotic time complexity of boo?

\(\Theta(n^2)\) Show Answer

Suppose a collection of unique numbers is stored in a balanced binary search tree, and that each node in the tree has been given a .size attribute which contains the number of nodes in the subtree rooted at that node. What is the time complexity required of an efficient algorithm for computing the number of elements in the collection which are larger than some threshold, \(t\)?

\(\Theta(\log n)\) Show Answer

What is the time complexity of the following function in terms of \(n\)? State your answer using asymptotic notation (e.g., \(\Theta(n)\)) in the simplest terms possible.

def foo(n):
    for i in range(n):
        for j in range(2023):
            for k in range(n - i):
                print("DSC40B")

\(\Theta(n^2)\) Show Answer

Suppose numbers is a list of integers of length \(n\). What is the time complexity of the following function in terms of \(n\)? State your answer using asymptotic notation (e.g., \(\Theta(n)\)) in the simplest terms possible.

def foo(numbers):
    for x in numbers:
        r = max(numbers) * min(numbers) * x
        print(r)

\(\Theta(n^2)\) Show Answer

What is the time complexity of the following function in terms of \(n\)? State your answer using asymptotic notation (e.g., \(\Theta(n)\)) in the simplest terms possible.

def foo(n):
    i = 1
    while i < n**3:
        i = i * 2
        for j in range(n):
            print(i + j)

\(\Theta(n\log n)\) Show Answer

Suppose a collection of \(n\) numbers is stored in a balanced binary search tree. What is the time complexity required of an efficient algorithm to calculate the mean of the collection? State your answer as a function of \(n\) in asymptotic notation.

\(\Theta(n)\) Show Answer

What is the expected time complexity of the function below? State your answer using asymptotic notation.

import random
def foo(n):
    # draw a number uniformly at random from 0, 1, 2, ..., n-1 in Theta(1) time
    x = random.randrange(n)
    if x < 20:
        for i in range(n**3):
            print("Very unlucky!")
    elif x < n / 2:
        for i in range(n):
            print("Unlucky!")
    else:
        print("Lucky!")

\(\Theta(n^2)\) . Show Answer

What is the time complexity of the following function in terms of \(n\)? State your answer using asymptotic notation (e.g., \(\Theta(n)\)) in the simplest terms possible.

import math
def foo(n):
    for i in range(3 * n**3 + 5 * n * math.ceil(math.log(n))):
        for j in range(math.floor(math.sqrt(n))):
            print(i + j)
        for k in range(n**2):
            print(k * i)

\(\Theta(n^5)\) Show Answer

Suppose bar_1, bar_2 and bar_3 are three functions. Suppose bar_1's time complexity is \(\Theta(n)\), bar_2's time complexity is \(\Theta(n^2)\), and bar_3's time complexity is \(\Theta(n^3)\).

Suppose foo is defined as below:

def foo(n):
    if n < 2023:
        bar_1(n**3)
    elif n == 2023:
        bar_3(n**2)
    else:
        bar_2(n)

What is the asymptotic time complexity of foo?

\(\Theta(n^2)\) Show Answer